Insertion sort algorithm

Insertion sort is probably the simplest sorting algorithm. You start with one element, and simply add new elements one at a time, in the correct place, until all the elements are sorted.

Simple version

Here is the simplest version of an insertion sort. We are going to sort these cards in ascending order:

We take the first card, the 9, and use it to start a new row of cards:

Then we take the next card, the 3, and move it to the correct position in the new row - 3 is less than 9, so it goes to the left of the 9.

The next card, 6, is moved its correct position, between the 3 and the 9.

The next card, 5, is moved its correct position, between the 3 and the 5.

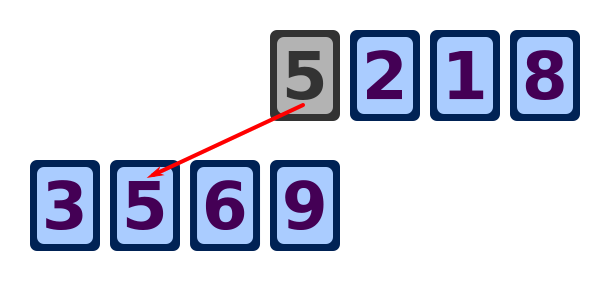
And so on, until all the cards have been moved from the top row to the bottom row. The cards will now be in order.

"In place" algorithm

The algorithm described above uses 2 arrays, one for the input values, another for the sorted output values. But the algorithm can also be carried out in-place, using the same array for the input values and the output values.

Here is a video showing the algorithm:

Pseudo code

Now we can try to write some pseudo code for the algorithm. First lets take an overview. Remember that we number array elements starting at zero. The process is:

• Take element 1 (the 3 card) and move it to its sorted position.
• Take element 2 (the 6 card) and move it to its sorted position.
• Take element 3 (the 5 card) and move it to its sorted position.
• Keep going to the end of the array.

As a loop we can say:

for i = 1 to length(k)-1
    move element k[i] to its sorted position

Now we need to fill in the detail of exactly how we move each element to its sorted position. As an example, consider the case when j (the element index) is 3:

We compare k[j] with k[j-1], and if k[j] is less, we swap the two elements. Now the element is in position 2, and we do the same thing again:

We keep comparing and swapping the element while ever it is less than the element top the left. However, if we reach the left hand end of the list (j = 0) we must also stop.

We can code this as:

j = 3
while k[j]<k[j-1] and j > 0
    swap k[j] and k[j-1]
    j = j - 1

This loop handles the case for element number 3. We need to sort every element, so we combine this code with the main loop above:

for i = 1 to length(k)-1
    j = i
    while k[j]<k[j-1] and j > 0
        swap k[j] and k[j-1]
        j = j - 1

See also

• Computational thinking
• Decomposition
• Recognising patterns
• Abstraction
• Using algorithms
• Search algorithms
• Linear search
• Binary search
• Search algorithms - resources
• Sort algorithms
• Bubble sort algorithm
• In-place algorithms
• Sorting algorithms - resources