Notes and octaves

A musical note is a sound with a particular frequency. In electronic music, the frequencies are defined precisely.

This article is about modern, western musical notes. Historically note frequencies were less well defined, and other cultures use different systems.

Every musical note has a specific frequency. For example middle C on the piano (or any other instrument) is 261.63Hz, the D above it is 293.66Hz, E is 329.63Hz. There is a pattern to this, as we will see below.

Note names

Here is a section of a standard piano keyboard:

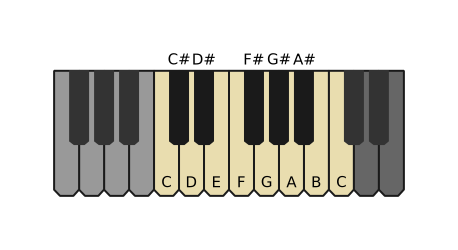
There are 12 different notes on the keyboard. In order (starting with C), they are C, C#, D, D#, E, F, F#, G, G#, A, A#, B.

The frequencies of these notes are equally spaced (but on a logarithmic scale as we will see). That is to say, the difference in frequency between any two adjacent notes sounds the same.

The are 7 notes with letter names (C, D, E, F, G, A, B) are called the natural notes. They are the notes of the C major scale, and occupy the white keys on the keyboard. This is the first scale you will probably learn when you start to play a piano or guitar. Many songs only use these notes.

The remaining notes (C#, D#, F#, G#, A#) are the sharps, and occupy the black keys. The notes E and B do not have sharps.

Sharps are sometimes added to the natural notes, even if the main scale if C major, and in that case they are sometimes called accidentals. They aren't accidental, of course, the composer used those notes deliberately, it is just a term to indicate that they are not part of the normal scale.

Some styles, such as jazz or blues, have their own scales which use a different mix of notes.

Since the gap between any two notes is one semitone, it follows that the gap between C and D is two semitones (or one tone), because there is a C# between them. In fact most of the notes in the major scale are separated by two semitones. E and F are separated by one semitone because there is no E# (so the two white keys have no black key between them). The same is true of B and C.

Octaves

The same pattern of 12 keys is repeated several times over the length of the piano keyboard:

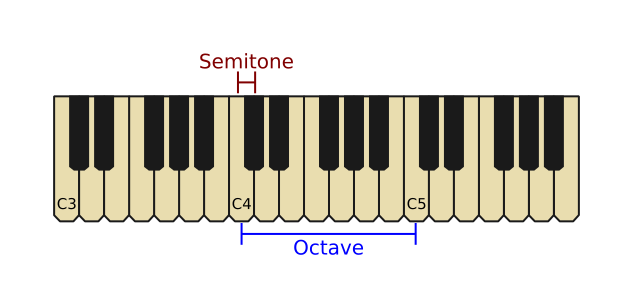
On each octave, the note in the same position is given the same name. So there are several different C notes.

When we move up an octave, every note has twice the frequency of the corresponding note in the previous octave. Similarly, when we move down an octave, every note has half the frequency of the corresponding note in the octave above.

We give the notes numbers to identify them. The C in the middle of the keyboard is called C4. It is also often called middle C for obvious reasons. C4 is also the note that is drawn halfway between the bass and treble staffs in sheet music.

The next C note along the keyboard, C5, has a frequency that is twice as high as middle C. The one after that is twice as high again, and so on. If we go in the opposite direction, the note C3, that is below C4 is half the frequency.

One thing to be aware of is that octave numbering starts at C. So D4 is higher than C4, but also A4 and B4 are higher than C4.

When one note has twice the frequency of the other, they sound sort of like they are the same note, even though one is clearly higher than the other. When played together they always sound perfectly harmonious.

Note frequencies

The 12 notes in an octave are equally spaced - they are separated by one semitone each. But they are spaced logarithmically, because that is how our ears sense frequencies.

The frequency of each note is found by multiplying the previous note by approximately 1.059463. Notes spaced like this sound as if they are equally spaced.

We define A4 to have the exact frequency of 440Hz. Every other frequency is calculated by multiplying (or dividing) 440 by 1.059463 multiple times.

So for example C4 is 9 semitones below A4. If we divide 440 by 1.059463, 9 times, we get 261.63Hz.

What is the magic number 1.059463? It is actually the 12th root of 2. If we multiply this number by itself 12 times, we get 2:

1.059463 x 1.059463 x 1.059463 x ... 12 times = 2

This, of course, is exactly what we need because the frequency doubles every octave.

Flats and sharps

As we noted earlier, the white keys are called the natural notes. A black key is usually called a sharp and is named after the previous white key. For example the black key after a C note is called a C sharp (C#) because it is one semitone higher ("sharper") than C.

You will notice that C# is also a semitone lower than D. We sometimes call the note D flat (D♭). C# and D♭ are the exact same note, the black key between C and D.

Notes B and E don't have sharps, which also mean that C and F don't have flats.

See also

• Music basics
• Major scales