Binary search

If you have a set of cards which are sorted in ascending order, you can use a technique called binary search. This is faster than a linear search (especially if you are searching through a lot of data), but it only works if the cards are sorted.

A simple binary search

Once again we will search for card number 3, as we did in the linear search. But this time we will take advantage of the fact that the cards are sorted in ascending order. We turn over the middle card.

That card is a 6. Since that cards are in order, we now know that every card to the right of this card must also be at least 6 or greater. So we can eliminate all of those cards:

There are now 3 cards left. We turn over the middle card out of the remaining 3 cards:

That card is a 2. We now know that every card to the left of this card must also be at 2 or less. So we can eliminate all of those cards:

There is only one card left. Once again we select the middle card (there is only one card, but it still counts as the "middle" card):

We have found our card! Another example is shown in the video below:

Defining the computer algorithm

Now we need to define our inputs, and the outputs for every possible case.

Inputs

The inputs for this algorithm are the same as for the linear search, a list k, and a search value v.

Outputs

Exactly the same as linear search, we return the position of the v within k.

What happens if the value appears more than once in k? Consider this list:

[1, 3, 3, 3, 5, 6, 8, 8, 9]

If we search for a 3, which element will we find first? The answer isn't obvious, you would need to work through the algorithm, it could land on the first one, the last one, or the middle one, depending on where they are and how long the list is. To make our life easy, we will just specify that our algorithm will return the index of any one of the matching elements.

What if v isn't present in k? Looking back at the cards example, towards the end we have eliminated every card except one:

If that card had been a 4, we would have eliminated it - and there would have been no cards left. Out algorithm must detect this case, and return -1.

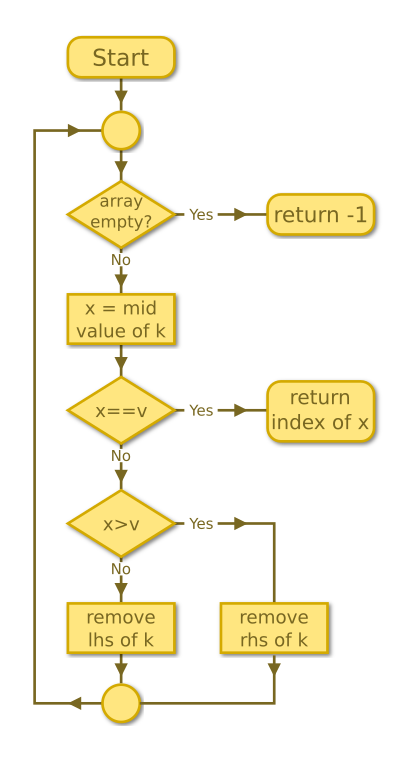
Pseudo code

Here is the algorithm in pseudo code:

INPUTS k, v
WHILE k is not empty
    SET x = mid element of k
    IF x equals v
        RETURN index of x
    ELSE IF x greater than v
        REMOVE right half of k
    ELSE
        REMOVE left half of k

RETURN -1

When we talk about removing the left or right half of k, that doesn't necessarily mean deleting those values from the list.

It might be more efficient to leave the items in the list, but ignore them after they have been eliminated. This is what happens in the example above using numbered cards.

If a matching element is not found, the loop ends and the final line of pseudo code returns -1.

Flowchart

See also

• Computational thinking
• Decomposition
• Recognising patterns
• Abstraction
• Using algorithms
• Search algorithms
• Linear search
• Search algorithms - resources
• Sort algorithms
• Insertion sort algorithm
• Bubble sort algorithm
• In-place algorithms
• Sorting algorithms - resources