Functional programming - what are functions?

Functions are very important in functional programming, so let's take a closer look at exactly what a function is.

Pure functions

In functional programming we use pure functions. A pure function is a function that:

• Has no side effects
• For a given set of inputs, always returns the same output value

Referential transparency

A side effect is anything that can effect the rest of the system. If a function sets a global variable, or interacts with other code or objects that might have effects beyond the function itself, that is a side effect, and it means that the function is not a pure function.

There are other types of side effect. For example if the function writes to a file, sends data across the network, that is also a side effect.

To be guaranteed free of side effects, a function should only call other pure functions (or operators that have no side effects).

Pure functions have referential transparency. This simply means that if you remove a call to the function, and replace it with the result of the call, the program will still do exactly the same thing. For example, assuming that square is a pure function that returns the square of a value, consider this code:

x = square(3)

This does exactly the same thing as the following code (they both set x to 9)

x = 9

But what about this code, assuming set_date sets a global date variable and returns 1 for success:

y = set_date("25-05-2018")

and

y = 1

They both set y to 1, but the first one also sets a global variable. setdate does not have referential transparency, because you can't just replace the function call with its return value.

Statelessness

Pure functions are stateless. They depend on nothing except their input parameters. So square(3) will always return 9, under all circumstances.

If we had a function get_date that read a date out of the same global variable that set_date uses, we have no idea what value we might get back. It will just be whatever the last call to get_date happened to put there.

Advantages of pure functions

There are some clear advantages to pure functions. The first is predictability. We know exactly what a function will return. This means that our code is less likely to have bugs (and required less testing).

Another is order dependency. For example:

a = square(4)
b = square(5)

if we did this the other way round:

b = square(5)
a = square(4)

we still get the same result, a is 16 NS b is 25. But what about this code:

set_date("25-05-2018")
c = get_date()

if we do that the wrong way round:

c = get_date()
set_date("25-05-2018")

we have no idea what is in variable c, but it will most likely be incorrect.

This leads on to another question. What happens in a multiprocessor (or multithreaded) case if you call the functions at the same time?

If you call square from different threads at the same time, it shouldn't cause any problems. Both calls to square are sharing the code but they have their own separate variables so nothing will go wrong.

What if you call get_date from a different thread at the same time as set_date? Well set_date could be half way through updating the global date variable, so get_date might read totally invalid data. To avoid this you would have to take special measures to make the functions thread safe.

These sorts of problems are often a major source of difficult to find bugs in software. You can't eliminate them completely (sometimes you actually need two threads to share data) but functional programming greatly reduces the problem.

Domains and co-domains

So a pure function takes one or more input parameters, and produces an output value that depends only on the inputs.

We could think of it as a function machine that takes a set of inputs and produces an output:

Every possible combination of inputs creates a particular output. We could say that the function machines maps each possible set of inputs onto one particular output.

This is a many-to-one mapping. For example, using the square function, input value 2 always creates an output of 4. But an input of -2 also produces an output of 4. Each input results in a specific output, but many different inputs can create the same output.

Some functions can only accept a certain set of input values. The set of allowable input values is called the domain of the function. This set of inputs will produce a set of possible output values, called the co-domain of the function.

Although these examples use numbers as input and output values, remember that a function can operate on any type of data - numbers, strings, list and so on.

Examples

We will now look at some example functions, with their domains and co-domains.

The square function

First the square function we have used as an example before. In Python this looks like:

def square(x):
    return x*x

And here is a graph (produced with the wonderful matplotlib):

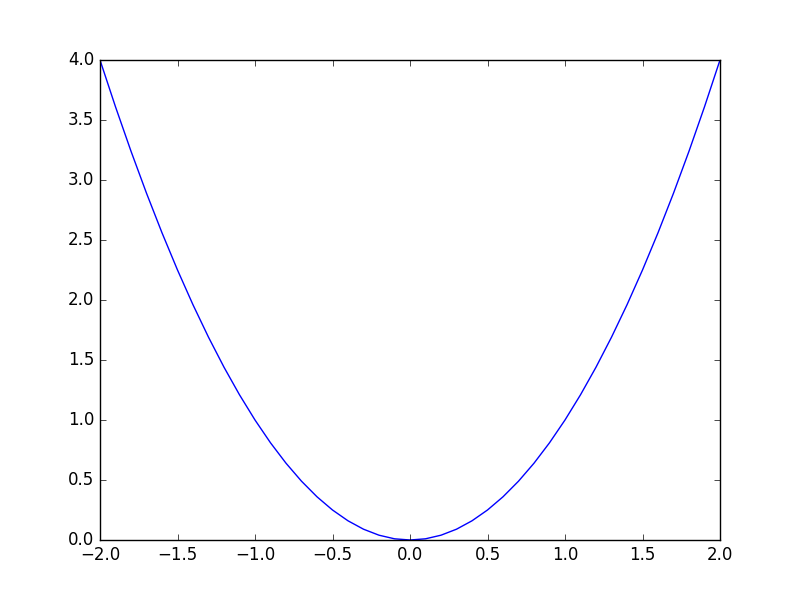
Clearly you can pass any real number into the square function (we won't worry about complex numbers here). So the domain of the function is the set of all real numbers. Mathematicians use the symbol ℝ for this ste, but we are programmers not mathematicians.

Of course, the result of the square function is always non-negative, so the co-domain of the square function is the set of all real numbers greater than or equal to 0.

The modulo function

As a second example we will look at the modulo function, specifically modulo 7 (for no particular reason). In Python this is

def modulo7(x):
    return x % 7

The modulo operator (% in Python) returns the remainder when x is divided by n (7 in this case). We will stipulate that x must be an integer, although actually Python modulo can work with float values. Here is a graph of the function:

Clearly the remainder when you divide a number by 7 has to be somewhere between 0 and 6, so:

• The domain is the set of all integers
• The co-domain is the set of integers {0, 1, 2, 3, 4, 5, 6}

The inverse sine function

The inverse sine function (or arcsine as it is sometimes called) is used in trigonometry to find the angle in a triangle based on its sides. The formula is:

angle = arcsine(opposite/hypotenuse)

We will stick with the simple geometric version of the formula, based on right angled triangles. Since the hypotenuse is the longest side of the triangle, the input value can never be greater than 1. It can never be less than 0, because the length of a side cannot be negative (in our simple geometric interpretation).

On the other hand, the angle can never be greater than 90 degrees (because it is a right angled triangle, so it can't have obtuse angles). And the angle can't be less than 0 because angles can't be negative is good old fashioned geometry.

Here is the graph:

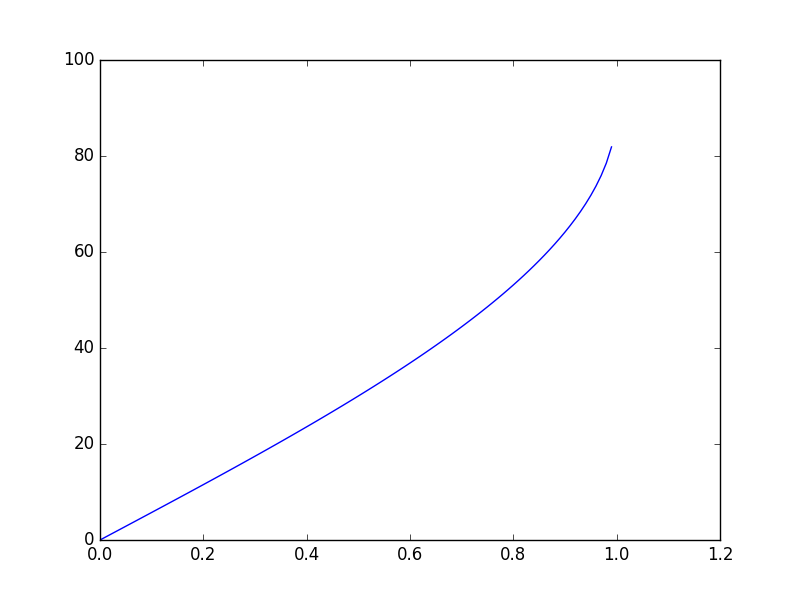
In this case:

• The domain is any real number between 0 and 1
• The co-domain is any real number between 0 and 90

See also

• Functional programming